2021. 9. 1. 02:27ㆍai/Machine Learning

Nomalization (정규화)
데이터가 가진 scale(규모, 등급)이 심하게 차이가 나는 경우 학습이 잘 안 이루어지지 않아요
scale [즉 중요도]을 맞춰주는 작업이 필요 → Nomalization
ex) 집의가격 (똑같은 숫자라도 중요도가 다르다)
- 방의개수 : 1 ~ 20
~ 연식(월) : 1 ~ 240 (20년)
정규화 방식이 많지만 그중 두개
# z - score Normalization (standardizaion 표준화 라고도 불린다)
# Min - Max Normalization (가장 일반화된 방식)
-모든 feature에 대해 최소값 0 최대값 1 사이의 값으로 scaling
-편하고 간편하지만 이상치에 상당히 민감하므로 무조건 이상치 처리해야한다
Xscaled = X - X(min) / X(max) - X(min) [ 분모 ]
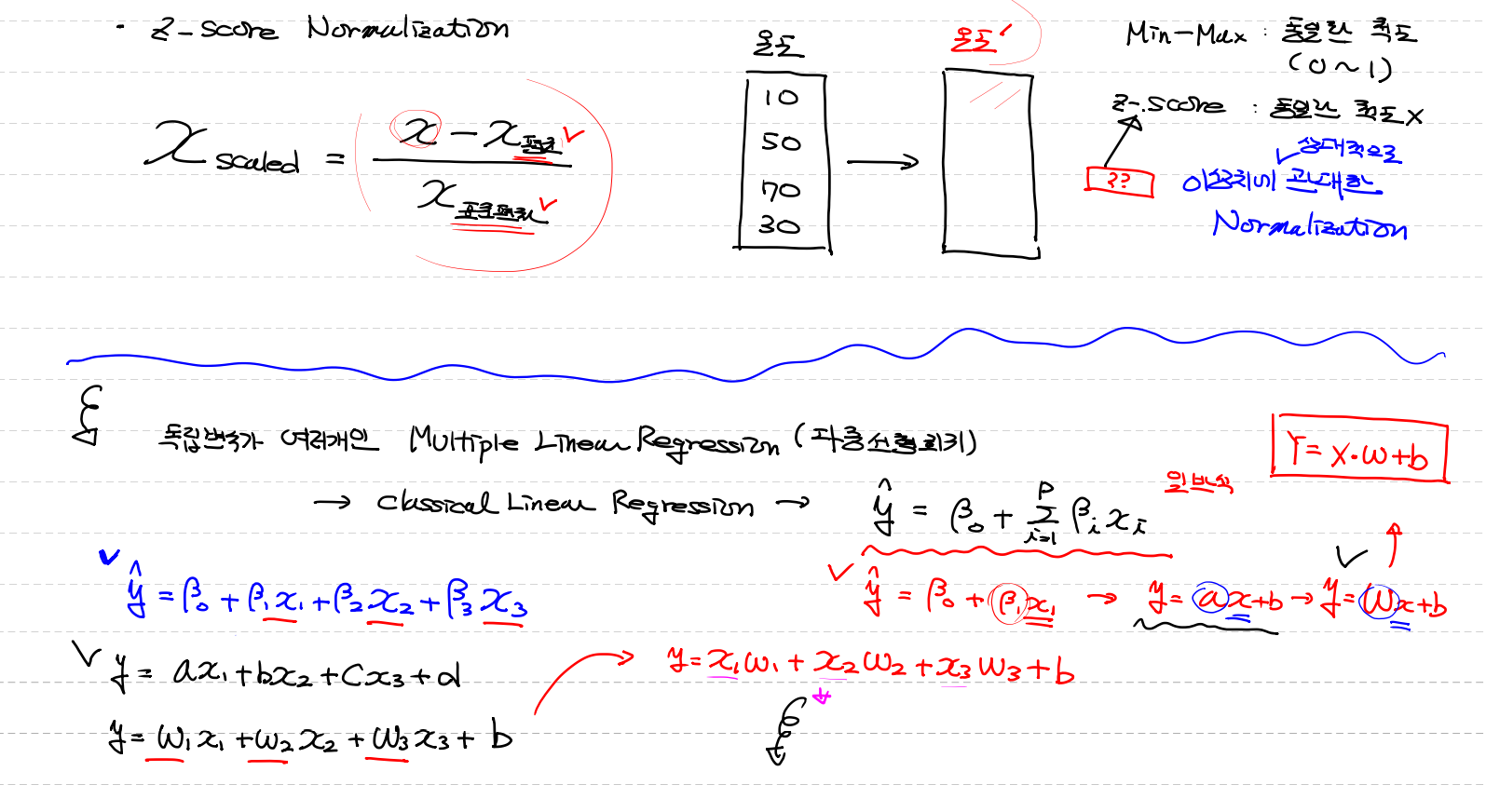
# z - score Normalization (standardizaion 표준화)
Xscaled = X - X평균 / X표준편차 이므로 음수가 나올수있다
Min - Max Normalization : 0과1이라는 동일한 scale척도
z - score Normalization : 동일한 척도x / 이상치에 많은 영향을 안받는다 (평균과 표준편차를 이용해서)
ㅡㅡㅡㅡㅡㅡㅡㅡㅡㅡㅡㅡㅡㅡㅡㅡㅡㅡㅡㅡㅡㅡㅡㅡㅡㅡㅡㅡㅡㅡㅡㅡㅡㅡㅡㅡㅡㅡㅡㅡㅡㅡㅡ
독립변수가 여러개인 Multiple Linear Regression (다중선형회기)

기존 독립변수가 1개일때


import numpy as np
import pandas as pd
import matplotlib.pyplot as plt
from sklearn import linear_model
from scipy import stats # z-score를 이용해 이상치 처리
from sklearn.preprocessing import MinMaxScaler # MinMaxScaler 정규화 처리
### 수치미분함수 ###
def numerical_derivative(f, x):
delta_x = 1e-4
derivative_x = np.zeros_like(x)
it = np.nditer(x, flags=['multi_index'])
while not it.finished:
idx = it.multi_index
tmp = x[idx]
x[idx] = tmp + delta_x
fx_plus_deltax = f(x)
x[idx] = tmp - delta_x
fx_minus_deltax = f(x)
derivative_x[idx] = (fx_plus_deltax - fx_minus_deltax) / (2 * delta_x)
x[idx] = tmp
it.iternext()
return derivative_x
##############################################
# Raw Data Loading
df = pd.read_csv('./data/ozone/ozone.csv', sep=',')
training_data_set = df[['Temp', 'Ozone']]
# display(training_data_set.head())
# 1. 결치값부터 처리해야 해요!
training_data = training_data_set.dropna(how='any')
# inplace = True 는 원본삭제인데 좋은 방법은 아니다
# display(training_data.shape) # (116, 2)
# 2. 이상치를 처리해야 해요!
zscore_threshold = 1.8
[broadcasting을 위해 위와같이 표현]
# Temp에 대한 이상치(지대점) 처리
outlier = training_data['Temp'][np.abs(stats.zscore(training_data['Temp'])) > zscore_threshold]
# np.abs:절대값으로 / stats.zscore(): zscore값 구하기
# print(outlier) # 지대점
training_data = training_data.loc[~(training_data['Temp'].isin(outlier))] # 110 rows × 2 columns
~() : 역으로 바꿔준다
# Ozone에 대한 이상치(outlier) 처리
outlier = training_data['Ozone'][np.abs(stats.zscore(training_data['Ozone'])) > zscore_threshold]
training_data = training_data.loc[~(training_data['Ozone'].isin(outlier))]
# display(training_data) # 103 rows × 2 columns
# 3. Normalization(정규화) - Min-Max Normalization
scaler_x = MinMaxScaler() # scaling 작업을 수행하는 객체를 하나 생성
# (입력값처리하는놈1개, label처리하는놈 1개)
scaler_y = MinMaxScaler()
scaler_x.fit(training_data['Temp'].values.reshape(-1,1)) # 데이터의 개수, 최대, 최소 같은 값들의 정보를 minmax class에 전달
# scaler에 저장 #무조건 metrix 2차원
scaler_y.fit(training_data['Ozone'].values.reshape(-1,1))
# 2차원 matrix로 들어가야한다
training_data['Temp'] = scaler_x.transform(training_data['Temp'].values.reshape(-1,1))
training_data['Ozone'] = scaler_y.transform(training_data['Ozone'].values.reshape(-1,1))
# transform() : 변환한다
# display(training_data)

#################전처리 완료
# Training Data Set
x_data = training_data['Temp'].values.reshape(-1,1)
t_data = training_data['Ozone'].values.reshape(-1,1)
# Weight & bias를 정의
W = np.random.rand(1,1)
b = np.random.rand(1)
def predict(x):
return np.dot(x,W) + b # y = Wx + b
def loss_func(input_obj): # [W의 값, b의 값] 1차원 ndarray
input_w = input_obj[0].reshape(-1,1) # 행렬곱연산을 수행해야 하니까 2차원으로 표현
input_b = input_obj[1]
# 평균제곱오차를 구해야 해요! => loss함수의 값.
y = np.dot(x_data,input_w) + input_b # 입력값에 대해 현재 W와 b를 이용한 예측치 계산
return np.mean(np.power((t_data-y),2))
learning_rate = 1e-4
# 반복학습을 진행
for step in range(300000):
input_param = np.concatenate((W.ravel(), b.ravel()), axis=0)
result_derivative = learning_rate * numerical_derivative(loss_func,input_param)
W = W - result_derivative[0].reshape(-1,1)
b = b - result_derivative[1]
if step % 30000 == 0:
print('loss : {}'.format(loss_func(input_param)))
# 학습이 끝났으니 Prediction을 해 보아요!
# print(predict([[62]])) # [[48.74690939]] ???? 많이 이상해요!!! ㅡㅜ 당연히 이상한거예요!
#data를 Nomalizaion(정규화)를 했기 때문이다 그래서 다시 바꿔줘야한다
scaled_predict_data = scaler_x.transform([[62]])
print(scaled_predict_data)
scaled_result = predict(scaled_predict_data) ## [[-0.02019973]] ?? 이게 최종 예측값인가요??
# 원래값으로 복구해야해요!
print(scaler_y.inverse_transform(scaled_result)) ##[[2.12142534]]
#inverse 가 역으로라는 뜻을 가진다
# sklearn을 이용한 구현
df = pd.read_csv('./data/ozone/ozone.csv', sep=',')
training_data_set = df[['Temp', 'Ozone']]
# display(training_data_set.head())
# 1. 결치값부터 처리해야 해요!
training_data = training_data_set.dropna(how='any')
# 2. 이상치를 처리해야 해요!
zscore_threshold = 1.8
# Temp에 대한 이상치(지대점) 처리
outlier = training_data['Temp'][np.abs(stats.zscore(training_data['Temp'])) > zscore_threshold]
# print(outlier) # 지대점
training_data = training_data.loc[~(training_data['Temp'].isin(outlier))] # 110 rows × 2 columns
# Ozone에 대한 이상치(outlier) 처리
outlier = training_data['Ozone'][np.abs(stats.zscore(training_data['Ozone'])) > zscore_threshold]
training_data = training_data.loc[~(training_data['Ozone'].isin(outlier))]
model = linear_model.LinearRegression()
model.fit(training_data['Temp'].values.reshape(-1,1),
training_data['Ozone'].values.reshape(-1,1))
result = model.predict([[62]]) # [[3.58411393]]
print(result)
## 그래프를 그려보아요!
#################################
fig = plt.figure()
fig_python = fig.add_subplot(1,2,1)
fig_sklearn = fig.add_subplot(1,2,2)
fig_python.set_title('Using Python')
fig_sklearn.set_title('Using sklearn')
#################################
fig_python.scatter(x_data,t_data)
fig_python.plot(x_data, x_data*W.ravel() + b, color='r')
fig_sklearn.scatter(training_data['Temp'].values,
training_data['Ozone'].values)
fig_sklearn.plot(training_data['Temp'].values,
training_data['Temp'].values*model.coef_.ravel() + model.intercept_, color='g')
fig.tight_layout()
plt.show()
# 독립변수가 3개인 multiple Linear Regression을 구현해 보아요!
import numpy as np
import pandas as pd
import matplotlib.pyplot as plt
from sklearn import linear_model
from scipy import stats
from sklearn.preprocessing import MinMaxScaler
### 수치미분함수 ###
def numerical_derivative(f, x):
delta_x = 1e-4
derivative_x = np.zeros_like(x)
it = np.nditer(x, flags=['multi_index'])
while not it.finished:
idx = it.multi_index
tmp = x[idx]
x[idx] = tmp + delta_x
fx_plus_deltax = f(x)
x[idx] = tmp - delta_x
fx_minus_deltax = f(x)
derivative_x[idx] = (fx_plus_deltax - fx_minus_deltax) / (2 * delta_x)
x[idx] = tmp
it.iternext()
return derivative_x
##############################################
# Raw Data Loading
df = pd.read_csv('./data/ozone/ozone.csv', sep=',')
# display(df)
training_data_set = df[['Solar.R', 'Wind', 'Temp', 'Ozone']]
# display(training_data_set.head())
# # 1. 결치값부터 처리해야 해요!
training_data = training_data_set.dropna(how='any')
# display(training_data.shape) # (111, 4)
# # 2. 이상치를 처리해야 해요!
zscore_threshold = 1.8
# # Ozone에 대한 이상치(outlier) 처리
outlier = training_data['Ozone'][np.abs(stats.zscore(training_data['Ozone'])) > zscore_threshold]
training_data = training_data.loc[~(training_data['Ozone'].isin(outlier))]
# display(training_data) # 104 rows × 4 columns
# 3. Normalization(정규화) - Min-Max Normalization
scaler_x = MinMaxScaler() # scaling 작업을 수행하는 객체를 하나 생성
# 입력값 x에 대한 전체 scaler이다
scaler_y = MinMaxScaler()
scaler_x.fit(training_data.iloc[:,:-1].values)
scaler_y.fit(training_data['Ozone'].values.reshape(-1,1))
training_data.iloc[:,:-1] = scaler_x.transform(training_data.iloc[:,:-1].values)
training_data['Ozone'] = scaler_y.transform(training_data['Ozone'].values.reshape(-1,1))
# display(training_data)
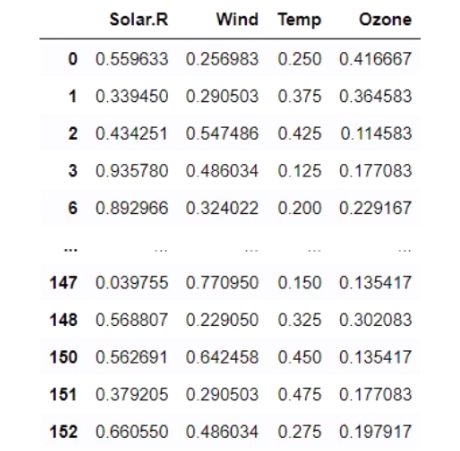
# Training Data Set
x_data = training_data.iloc[:,:-1].values
t_data = training_data['Ozone'].values.reshape(-1,1)
# Weight & bias를 정의
W = np.random.rand(3,1)
b = np.random.rand(1)
def predict(x):
return np.dot(x,W) + b # y = Wx + b
def loss_func(input_obj): # [W1의 값, W2의 값, W3의 값, b의 값] 1차원 ndarray
input_w = input_obj[:-1].reshape(-1,1) # 행렬곱연산을 수행해야 하니까 2차원으로 표현
input_b = input_obj[-1:]
# 평균제곱오차를 구해야 해요! => loss함수의 값.
y = np.dot(x_data,input_w) + input_b # 입력값에 대해 현재 W와 b를 이용한 예측치 계산
return np.mean(np.power((t_data-y),2))
learning_rate = 1e-4
# 반복학습을 진행
for step in range(300000):
input_param = np.concatenate((W.ravel(), b.ravel()), axis=0) # [W1의 값, W2의 값, W3의 값, b의 값]
result_derivative = learning_rate * numerical_derivative(loss_func,input_param)
W = W - result_derivative[:-1].reshape(-1,1)
b = b - result_derivative[-1:]
if step % 30000 == 0:
print('loss : {}'.format(loss_func(input_param)))
sklearn Multiple Linear Regression
model = linear_model.LinearRegression()
model.fit(training_data[['Solar.R','Wind','Temp']].values,
training_data['Ozone'].values.reshape(-1,1))
result = model.predict([[180,10,62]]) # [[11.0682182]]
print(result)
'ai > Machine Learning' 카테고리의 다른 글
| Logistic[논리] Regression (0) | 2021.09.02 |
|---|---|
| Tensorflow 1.대버전 (0) | 2021.09.02 |
| Sklearn(사이키런), 이상치처리 (0) | 2021.08.31 |
| ozone.csv를 python,sklearn으로 LinearRegression 처리 (0) | 2021.08.30 |
| LinearRegression 정리 (0) | 2021.08.30 |