2021. 9. 5. 21:12ㆍai/Machine Learning
data preprocessing - 데이터 전처리
1.결측치 : nan
2.이상치(outlier) : data의 일반적인 값보다 상대적으로 큰 data (평균에 영향을 많이 끼침)
- 독립변수 이상치 : 지대점, 지대값 / 종속변수 이상치 : outlier
- 사분위를 이용한 "Turkey Fence"
IQR ( Inter quartile range ) : 1사분위와 3사분위 사이를 지칭
IQR value : 3사분위값 - 1사분위값
matplotlib같은 visualieation modul (시각화 모듈) 은 Boxplat기능을 제공
-if "1사분위값(25%) - (IQR value * 1.5)" 이 값보다 더 작은 값은 "이상치"
-if "3사분위값(75%) + (IQR value * 1.5)" 이 값보다 더 큰 값은 "이상치"
print(np.percentile(data,50)) # 8.0 50 - 중위값
print(np.median(data)) # 8.0 중위값구하는 함수
이렇게 이상치를 판단하는게 Turkey Fence
# upper_bound : 상계(上界): 주어진 집합의 어떤 원(元)보다도 크거나 같은 값; 예를 들면 3과 4는 1, 2, 3을 원(元)으로 하는 집합의 상계이다.
lower_bound = np.percentile(data,25) - iqr_value * 1.5
- 정규분포와 표준편차를 이용한"Z-score"
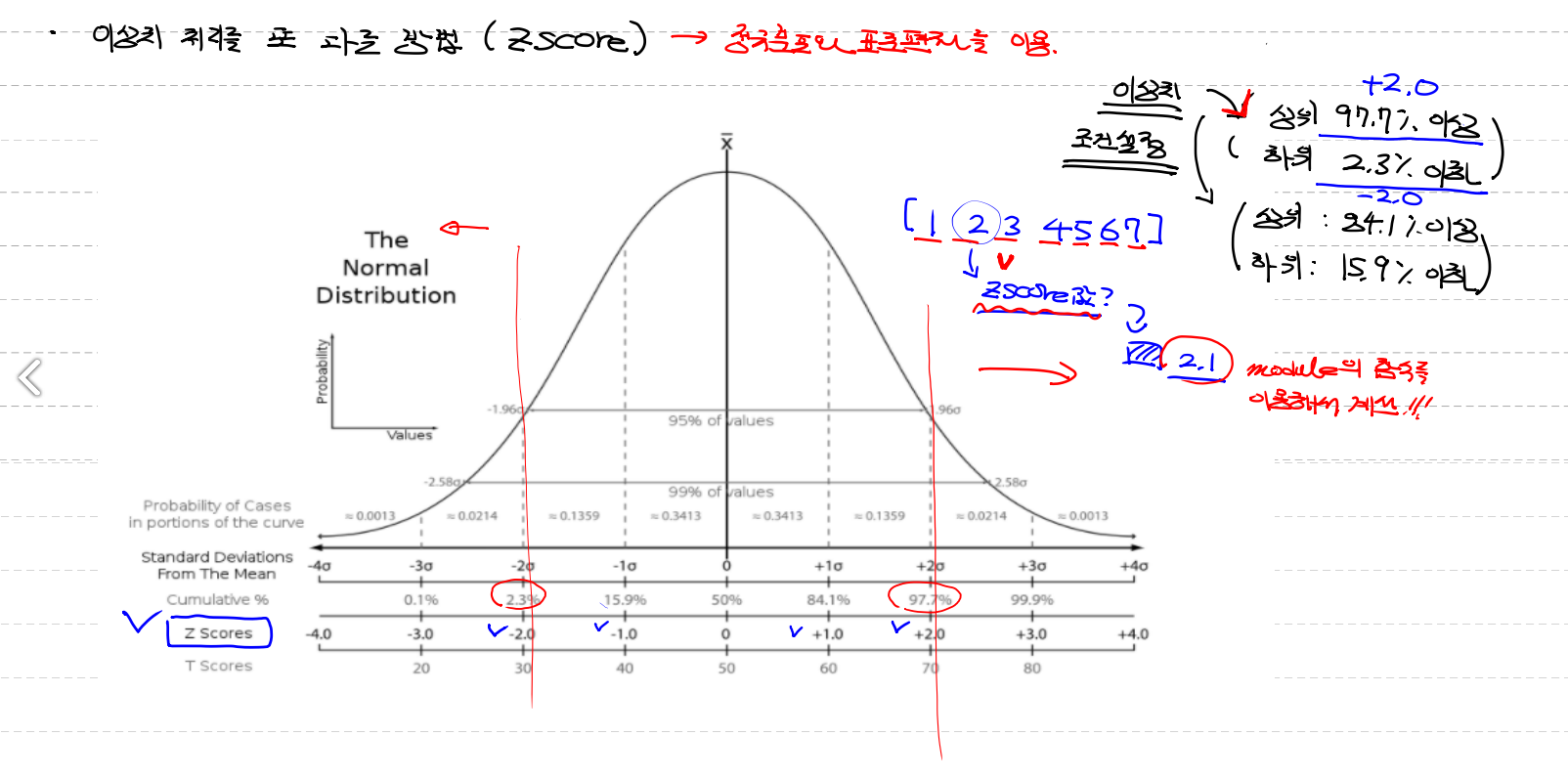
- data들을 정규분포로 나누어 data들의 각각을 z score로 나눈다 / z score구하는 식이 따로 있다
(modul의 함수를 이용해서)
from scipy import stats (통계)
zscore_threshould = 1.8 #zscore의 값을 설정
outlier = data[np.abs(stats.zscore(data)) > zscore_threshould] # 이상치값 구하기
# stats.zscore() : zscore 를 구해라
# np.abs() : 절대값으로 변경 (음수를 양수로) / threshould : 한계
# 이상치를 제거한 결과는
data[np.isin(data,outlier, invert=True)]
# np.isin : 여기안에 있니 ? 위는 data안에 outlier가 있니?
# invert=True # invert 역으로라는 뜻
3.Nomalization (정규화)
데이터가 가진 scale(규모, 등급)이 심하게 차이가 나는 경우 학습이 잘 안 이루어지지 않아요
scale [즉 중요도]을 맞춰주는 작업
ex) 집의가격 (똑같은 숫자라도 중요도가 다르다)
- 방의개수 : 1 ~ 20
~ 연식(월) : 1 ~ 240 (20년)
정규화 방식이 많지만 그중 두개
# z - score Normalization (standardizaion 표준화 라고도 불린다)
- 동일한 척도x / 이상치에 많은 영향을 안받는다 (평균과 표준편차를 이용해서)

# Min - Max Normalization (가장 일반화된 방식)
-모든 feature에 대해 최소값 0 최대값 1 사이의 값으로 scaling
-편하고 간편하지만 이상치에 상당히 민감하므로 무조건 이상치 처리해야한다
-0과1이라는 동일한 scale/(눈금) 척도, 저울질하다 / scaling : [컴퓨터] 크기 조정;
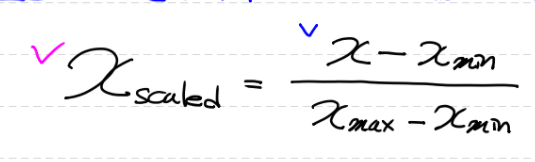
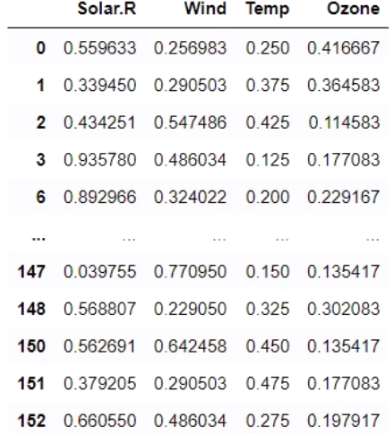
from sklearn.preprocessing import MinMaxScaler
scaler_x = MinMaxScaler() # scaling 작업을 수행하는 객체를 하나 생성
# (입력값처리하는놈1개, label처리하는놈 1개)
scaler_y = MinMaxScaler()
scaler_x.fit(training_data['Temp'].values.reshape(-1,1)) # 데이터의 개수, 최대, 최소 같은 값들이 scaler에 저장
scaler_y.fit(training_data['Ozone'].values.reshape(-1,1))
# 2차원 matrix로 들어가야한다
training_data['Temp'] = scaler_x.transform(training_data['Temp'].values.reshape(-1,1))
training_data['Ozone'] = scaler_y.transform(training_data['Ozone'].values.reshape(-1,1))
#transform(): 변환한다
scaled_predict_data = scaler_x.transform([[62]])
scaled_result = predict(scaled_predict_data) ## prediction 할때 nomalizaion으로 들어가야한다
# 원래값으로 복구해야해요!
print(scaler_y.inverse_transform(scaled_result)) ##[[2.12142534]]
#inverse 가 역으로라는 뜻을 가진다
| fit_transform (X [, y]) | 데이터에 맞추고 변환하십시오. |
독립변수가 여러개인 Multiple Linear Regression (다중선형회기)
model = linear_model.LinearRegression()
model.fit(training_data[['Solar.R','Wind','Temp']].values,
training_data['Ozone'].values.reshape(-1,1))
result = model.predict([[180,10,62]]) # [[11.0682182]]
print(result)
Tensorflow
- 1.대버전과 2.대버전이 있다 / 두 버전은 호환성이 없다 (외적으로는 많이 안변했으나 내부적으로는 많이 변함)
-도화지에 그래프를 그린다고 생각하면 된다
Node : Numerical computation(수치연산, data입출력 담당)
Edge : Node와 Node 사이에 data의 흐르는길
tensor :(동적크기의 다차원 배열: size,차원,길이가 얼만지모른다)연산을 해서 Edge를 통해 다른 Node로 흐르는 data
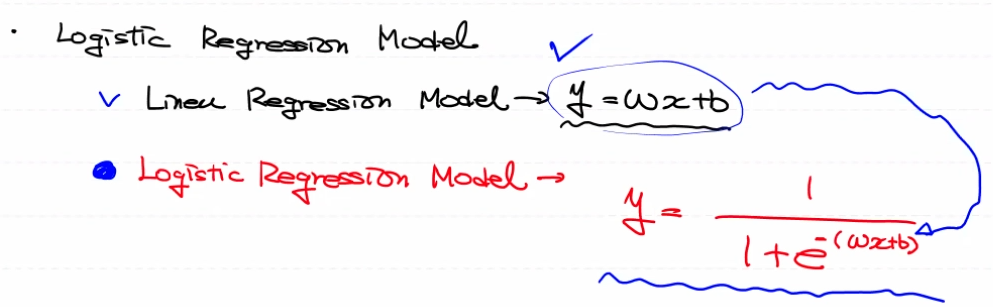
Logistic[논리] Regression
초창기 인공지능(1960년대) 알고리즘'Perceptron[퍼셉트론]'을 발전시킨 개념
Linear Regression(선형회기)을 확장해서 classification model
Machine Learning의 결과 model이 어떠한 값을 예측하는가 ?
Linear[선형, 직선] Regression (알고리즘) -Regression(회기 / model) → continuous[계속되는] value
Logistic[논리] Regression (알고리즘) -classification(분류 / model) → discrete[별개의] value
Activation[활성화] function : linear regration의 결과에 적용하는 함수
sigmoid(일반적으로 시그마라고 한다) : Activation function 의 대표적 함수로 x에 따라 y가 변환하는 함수로 y는 0 ~ 1
임계함수 Threshold Function : [결과값을 둘중하나로 분류, 연속값을 이상값으로 분류] (step function처럼 생겼다) →
Cross Entropy , log loss : - Logistic Regression Model 은 gradient descent algorism이 적용이 안된다
- Logistic Regression Model 의 loss function
- binaryClassfication(이진분류) , Multinomial Classfication(다중분류) 각각 다른식이다
- 원래의미는 Multinomial Classfication(다중분류) 의 lossfunction이나 편의상 binaryClassfication(이진분류) 에도 사용

1. Training Data Set
2. Linear Regression
3. classification (Sigmoid) [model]
4. Cross Entropy [log loss]
5. loss가 최적확인
6. 최적이면 END 아니라면 Weight, bias update"편미분"
'ai > Machine Learning' 카테고리의 다른 글
| 결측치처리 (0) | 2021.09.06 |
|---|---|
| Cancer 코드 Tensorflow ver (0) | 2021.09.06 |
| 1차 정리 (0) | 2021.09.05 |
| Cancer 코드 sklearn ver(k-fold) (0) | 2021.09.04 |
| data 전처리 / 생각해야 할 문제들 (0) | 2021.09.04 |